新里曼理论➋:共通音的网络
分享
上一节介绍了新里曼理论的基本要素。例如有名的“PLR操作”和“音网图”等等……
音网图的最小要素
另一方面,“六音循环”仍然值得深入挖掘。
这本身不过是用LP操作将6个和弦连接起来的环,但其本质是“有规律地重复半音差的和弦变形,通过串连制作出回到原来和弦的图”。这样的图,好像还有很多呢。 操作的模式不仅限于LP,可视化的方法也可以考虑圆环以外的方式,和弦的种类也没有决定限定于大和小的三和弦。这里还有无数的可能性。
1
Cube Dance
那么,将3个“基本PLR操作”并排在一起,但实际上只有1个被排除在外。
“其中一个会被排除在外~笑”
不用说,是唯一涉及全音差转换的R操作。在变形理论中,“声部联结的节俭”是关键之一,而这种差异在变形理论中意义重大。事实上,即使在六音循环中,也没有选择 R 操作。
采用aug
用稍微残酷的方式来说,R的变形被忽略了。将Rt移动半音为L,将3rd移动半音为P。现在我们来谈谈如何将5th移动半音。
是C⇄Caug的变形。如果我们抛开基于大/小和弦的音乐自然音阶观点,这种变换应该被视为相当于L/P操作的节俭变换操作。
aug的特殊性
而且aug有一个相当特殊的点,就是各音间隔相等,可以3个音都可视为根音。如果是Caug,就等于Eaug・A♭aug。这样一来,就会发现一些事。也就是说,不仅在 C和弦中,在E和弦和A♭和弦中,我们都可以通过将5th升半音来达到Caug。而说到C、E、A♭,它们正是前面提到的六音阶循环中出现的三个和弦。也就是说,六音循环所使用的3个主要三和弦,如果对5th进行变形的话就会变成单一的增三和弦!
(下文中,大和弦将用大写字母表示,小和弦用小写字母表示,这与提出这一建议的论文中的符号一致。这样就不会出现“+”与“aug”混淆的情况。)
这是一个很有趣的事实。这和“从上野到涩谷可以绕山手线,也可以穿过银座线”的构图很像。通过提到aug这种新的和弦类型,六音环的系统将变得更加复杂。
min和aug的关系
那么,小和弦和增和弦之间又是什么关系呢?一般来说,要想连接这两种和弦,要先提高3rd,然后再提高5th,大概需要“2步”,但其实不然。实际上存在“1步”就完成的方法。那是将Rt降低半音的变形。
这是Minor的低音线cliché的经典动作!正如所看到的,在日常使用中,存在着这样一个事实:aug是与大和弦和小和弦都只差一个音的和弦。正常理论将根音放在第一位,因此没有太多深入讨论这种关系。然而,将共同音放在首位的新里曼理论在这里发现了巨大的可能性。
和大和弦时一样,考虑到根音的替换,可以知道c、e、a♭这3个小和弦,如果把Rt降半音的话,全部都是Baug。也就是说,六音环的成员,小和弦的3个也会在aug(与3个大和弦不同)汇合。
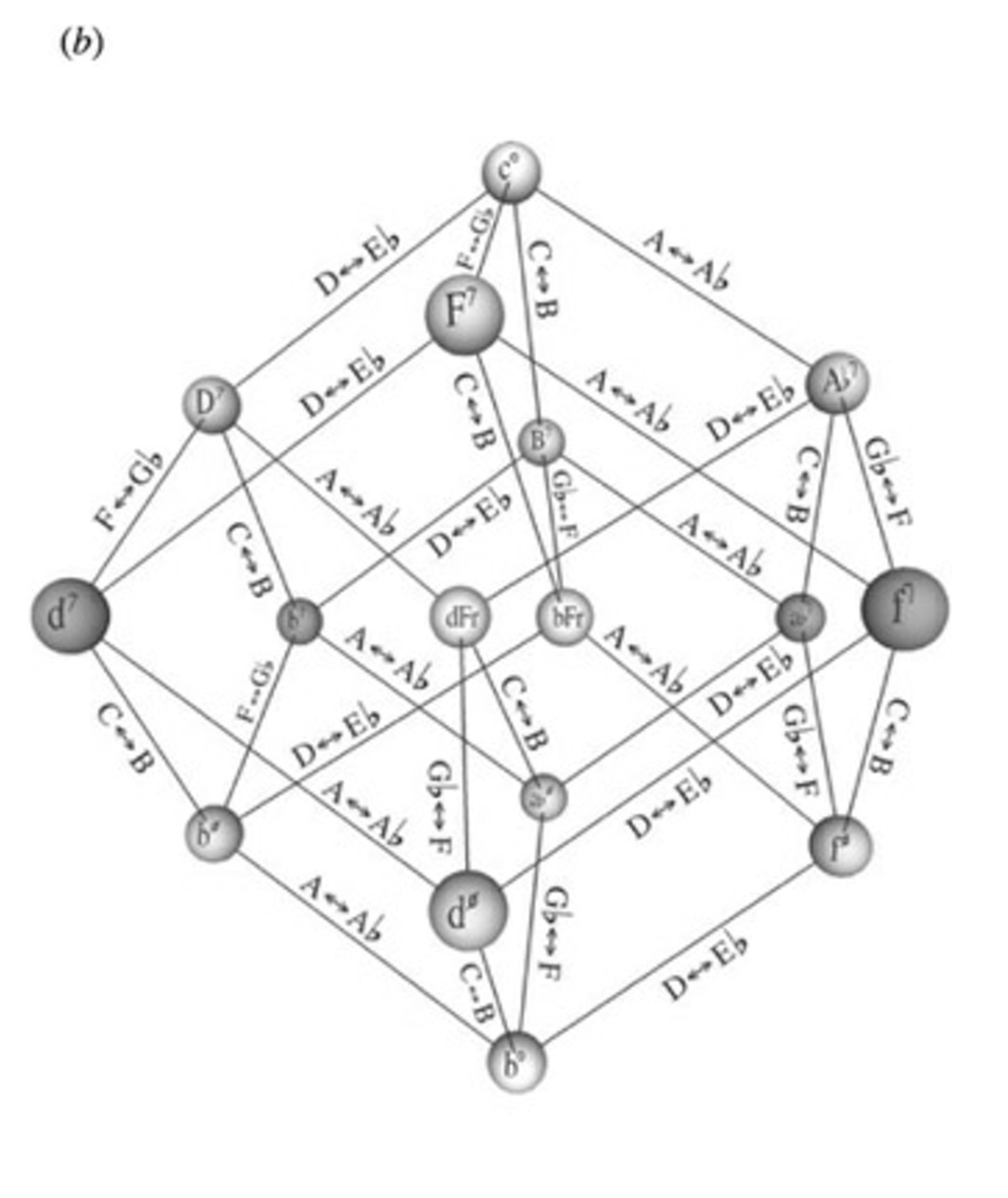
立方体化
3个大和弦,3个小和弦,2个aug,共8个和弦。这些构建了通过向特定方向移动Rt 3rd 5th来变形为8个中任意3个不同的和弦的密集网络。通过8个“点”和从各自延伸出来的3条“线”,整体相互连接……想要将这个可视化的时候,有最适合的图形,那就是立方体。
由于立方体的八个顶点都与三条边相连,因此更适合表达上述关系!原本的六音环被 打碎,变成了复杂的形状,但这是不可避免的牺牲,因为立体感带来的好处应该更大。
有趣的是,在这个立方体中,无论从哪一边看,向X(右)方向移动都会组成音g变为a♭,而向 Y(上)方向移动则为b→c,向Z(后)方向移动则e♭→e。这幅图有种浪漫的感觉,仿佛可以从这幅图中提出“aug是所有和弦之源”这样具有强烈思想性的理论。
“超六声系统”的4个环全部改造成立方体的话,会如下图所示。
(关于这次异名同音的拼写,我遵循了参考原论文的图画。)
现在,这样8×4=32个和弦集中在一个图上……虽然想这么说,但实际上并非如此。注意每个方块的aug,就会发现有重叠。B,A♭,F,D的aug分别出现了两次。
这也是理所当然的,一个aug在连接3个大和弦的同时也连接3个小和弦,所以每个都会有6个和弦的半音差连接。因此,在一个方块中与大和弦连接的aug并不能因此就省去了,还可以在另一个方块中进一步完成与3个小和弦连接的工作。
那么这样一来,图画中重复和弦一点都不漂亮。都这样了,不如再进一步。立方体,合体──
立方体的结合
稍微变形立方体的话,可以把重复的aug像“胶水”一样粘在一起,还可以像圆环状连接4个立方体。
咻!
这就是完成体!这张将4个立方体拉长并结合在一起的图,被称为{term:(英 {term:立方体舞蹈Cube Dance)1
*同一份文件中的注释指出:“立方体舞蹈这一名称是卡罗尔·克鲁姆汉斯尔在1993年纽约州立大学布法罗分校工作组会议上首次提出的。”可能是因为“舞蹈”一词是在会议上而不是在学术论文中诞生的,所以显得很随意。
Cube dance改造版
另外,虽然上面的图是参照论文中所描绘的内容,但如果将立方整体稍微歪曲一点,使对边全部平行的话,可能更容易把握与aug的距离感以及各操作的共通性。
咔咔咔
如果把它想象成一个充满张力的方块,就会让人无法静下心来,但如果把它想象成这种形状的水晶,就能以安静的心情去欣赏它了。
改造的时候顺便补充了一些细节信息。每个方块中平行关系的边的运动表示相同的声音变化,这一性质即使拉伸方块也不会改变,顺时针移动构成声音下行,逆时针移动构成一定要对应成音的上行。
因为cube dance的每一条边都表示一个半音的移动,所以从某条线到另一条线的变形量可以用边的移动数简单地测量,这一点是它的魅力所在。
当然,由于图中包含了aug,将能够直观地利用aug来构思和弦行进。
让cube dance离得更近
例如,使用aug和半音进行的例子有瓦格纳的《女武神骑行》。
歌剧歌手唱歌的和弦突然是Baug,这首先解决到了E。过了一会儿Baug又登场了,这次进入了C。
这在分析上可以用功能和声论充分解释,最初的Baug是对E为属的B的5th的“上方变形”。第二次也是把对C为属的G做成同样的aug化,再变成第一转位。两者都是D-T的功能进行,利用可以替换根音的aug的性质,从Baug这个单一和弦到E和C这两个不同的地方着陆。
……这么说倒也有道理,但如果问我自己能不能写出这样的过程,难度还是很高的。但是通过cube dance俯瞰半音连接的网络的话,Baug是比较容易连接到C和E这一信息,在理论理解之前首先从视觉上跳了出来。
如果是这样的话,可以用同样的距离去A♭,也可以从E和C反过来从A♭aug方向走到对面的cube,各种各样的行进模式的可能性马上就浮现出来了。就像“五度圈”提供了有关“五度进行”和“自然和弦”的各种视觉形象一样,“cube dance”也可以帮助我们想象“三度进行”和“共同音关系”。 新里曼理论现在主要作为分析工具而受到好评,但在制作方面,它也和“中心轴系统”一样能给人带来灵感。
2
Power Towers
到目前为止一直只针对三和弦,说到半音差的关系,在七和弦上也有。他们也是用半音差连接的。
而且像刚才一样,如果把“移动根音”的变形纳入其中的话,可以构建半减、小七、属七三种网络如下。
重点是向右下方向的变形,如果把Aø7的根音提高半音,就是Cm7的第三转位,把那根音提高半音,就是E♭7的第三转位。就这样,相隔小3度的根音的和弦连接在一起,然后从将八度分割为4的小3度的性质上看,经过4种跟音后又回到了原来的Am7。 因为这里只出现了C,E♭,F♯,A这4个跟音,所以其他连接C♯,E,G,B♭和D,F,A♭,B也都存在。
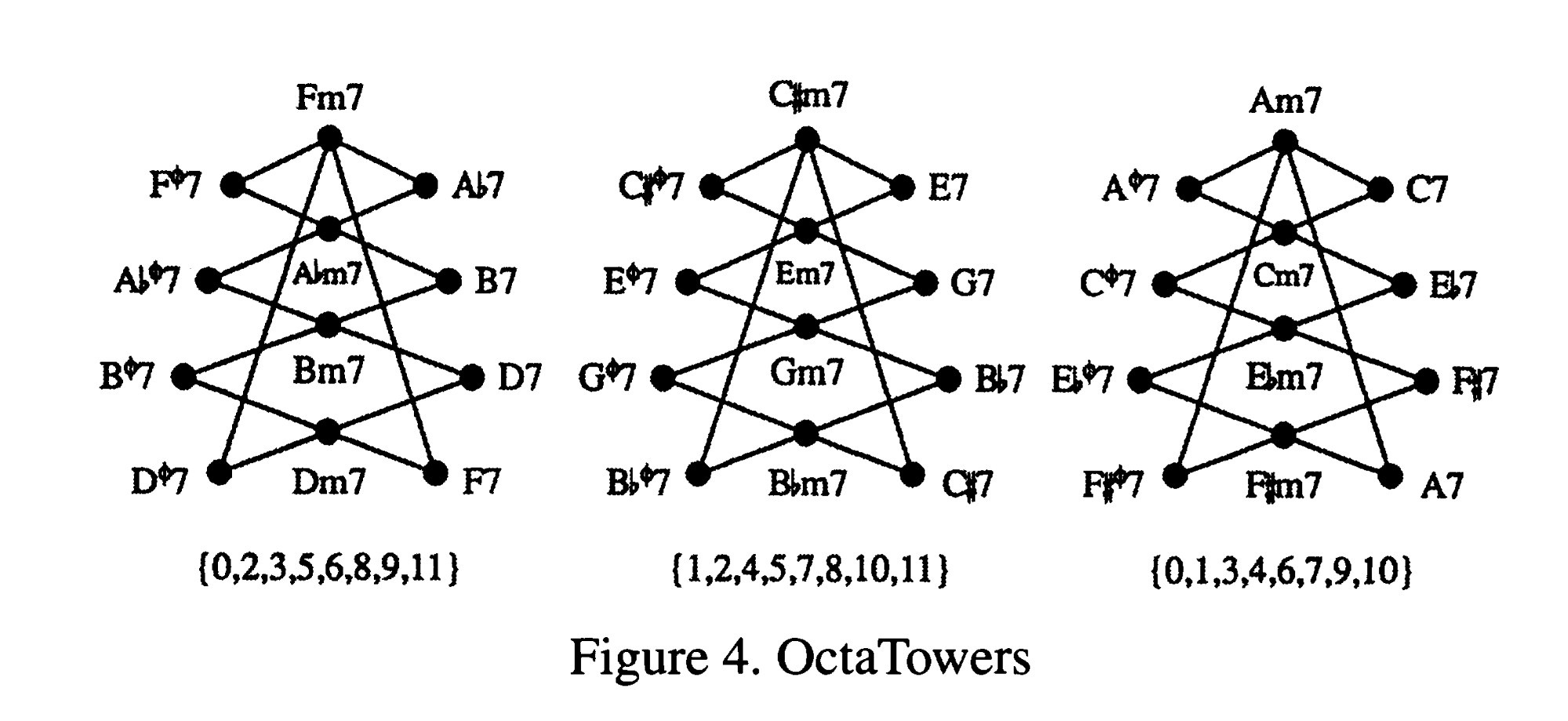
八音塔(Octatonic Tower)
因为好不容易有循环构造,所以也想做成循环的图形,不过,从有3列的状况变成圆环有点困难。因此,单纯地从下往上延伸线,就变成了电波塔的形状。
线条有交叉是缺点,不过作为图也十分简单明了。这张图叫做八音塔(英 Octatonic Tower)2
正如六音环的6个和弦仅由6个音的组合组成一样,八音塔的12个和弦仅由8个音组合组成,当它们放在一起时形成属减音阶(Dominant Diminished Scale)。
因为是由8个音组成的塔,所以叫Octatonic Tower(Octa代表八)。所以,C的属减音阶由Co7和C♯o7这两个dim7的和弦音组成。如果是这样的话,在上面提到的塔的图上加上这两个减七和弦似乎也不错。寻找与这些半音相连的和弦,构建网络……
会变成这样!半减七的7th降低的话当然是减七,但是即使是属七的Rt上移也是减七。这是像在V7→♯Vo7那样的进行中熟悉的知识。而且由于dim7特有的根音可换性,一个dim7可与4个和弦相连。
塔的结合
都到这里了,你是否注意到,这和刚才的cube dance几乎是同样的剧情呢?在上面的图中,Co7连接了半减七,但是也和其他的四个属七半音相连。它一定是另一座塔的成员,而dim7是两座塔之间的桥梁。就这样把大厦连接起来……
闪亮登场
会变成这样!!和cube dance一样,dim7通过与很多和弦的半音差连接的关系被很好地可视化了。这张图叫做超音塔(英 Power Towers)3
这个图示与刚才的cube dance图相反,顺时针方向的运动总是表示音的上行,逆时针方向表示下行。从这个意义上说,这个图左右反转可能会和刚才的Cube Dance图更有统一感。
添加大七的情况
另外,大七和弦也是基本和弦的一种却没被提及,以♯IVø7→IVΔ7为代表,从半减七通过降低根音连接,有着相当重要的特征。虽然没有dim7那样的集约性,但大七也有为这座塔架起最低限度的桥的能力。如果将其包括在内,总结成图的话,线会稍微交叉一点,但是可以像下面这样。
(*这是独家图案)
虽然没有aug7和mΔ7,但是可以把主要的七和弦的半音差网络汇总到平面上。除此之外,还有人提议将ø7和7中间的“法国六”添加到这个图内。
这样,就可以从不同的角度,如和弦的视野和连接等,进行真正意义上的多种可视化。新里曼理论中还有更多这样的图画,而将各种和弦网络可视化的尝试仍然是新里曼理论中的一个热门话题。
3
音乐理论的数学化
最后,作为新里曼理论的主题,它的内容已经和实践没有太大的关系了,那就是用数学的方式来描述音乐理论。
这是里曼本人在“新”之前的目标,特别是在1916年的《音想像論》中,他尝试用计算来表示和声的变形。
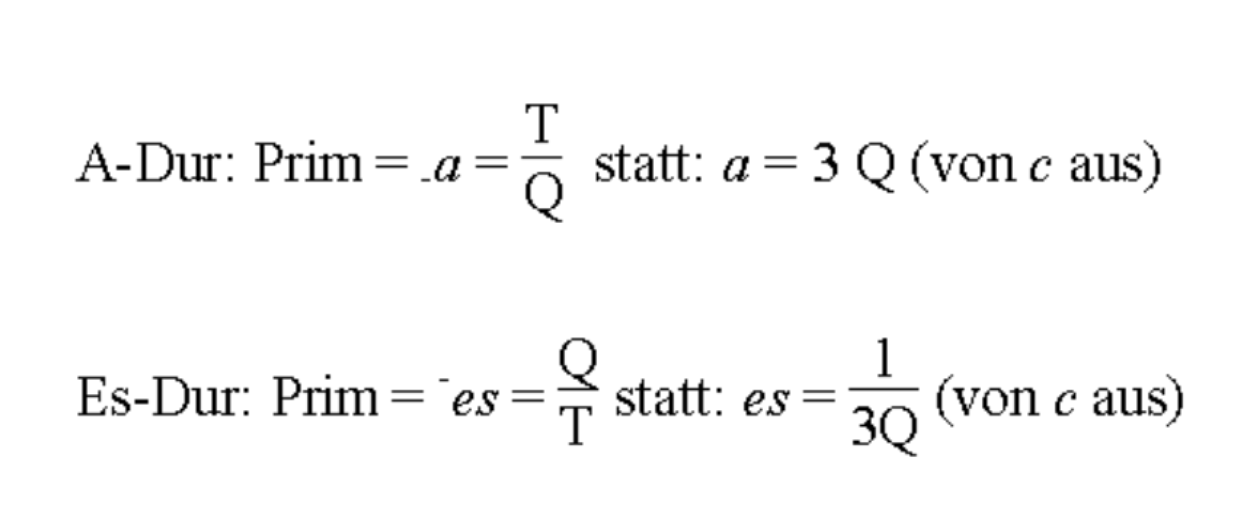
Riemann, Hugo. Ideen zu einer ‘Lehre von den Tonvorstellungen’.
这里Q是Quint表示“5度”,T是Terz表示“3度”,乘法(分子)表示上行,除数(分母)表示下行。
从C大和弦的角度来看,A大和弦是3Q,也就是“5度上行重复3次”的五度圈观点,而音网图认为是T/Q,也就是“3度上行和5度下行结合”的托内茨观点……就会展现出这样的场面。
上次也说过D操作的逆是D⁻¹,但是那种公式的举止是继承了里曼本人的遗志。
只是确实看上面的式子的话,a=T/Q这样用等号连接,左边是和弦,右边是和弦的进行,这有点不自然。Q,T是指对和声的变形操作,还是对和声本身的标签呢,情况很微妙。把“Q3”写成“Q³”而不是“3Q”,这也给人一种把“Q”单纯当作“5度”的数量来看待的感觉,这充分表现出了过渡期的感觉,以及想要抓住什么却还没有完成的感觉。
也许这就是评论家所说的,他并没有完全意识到自己在构思变形理论。里曼在这项工作完成三年后就去世了,享年70岁,因此甚至可以说,如果他再多活十年,他可能会亲自提出变形理论,这就更加令人遗憾了。因此,新里曼理论的主题之一就是继承他的遗志,将这一思想更进一步。为此,我将在本文中尝试介绍一些数学方面的内容。
音调级(Pitch Class)
首先,这个不局限于新里曼理论,更广泛使用的机制,用0~11的数字代替用ABC表示音名,这被称为音调级(英 Pitch Class,pc)(或音高级)。
| 音名 | C | C♯ | D | D♯ | E | F | F♯ | G | G♯ | A | A♯ | B |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| pc | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
音调级别是ABC音名的替代存在,和八度的高低没有关系。也就是说,例如pc=7的八度以上的音不设为pc=19,超过12的部分取余数同样设为pc=7。
通过数字,除了可以从数字上观察音的关系之外,在无视异名同音这一点上也有很大的意义,对于经常在没有调性的状态下讨论的新里曼理论来说,音调级是非常方便的存在。
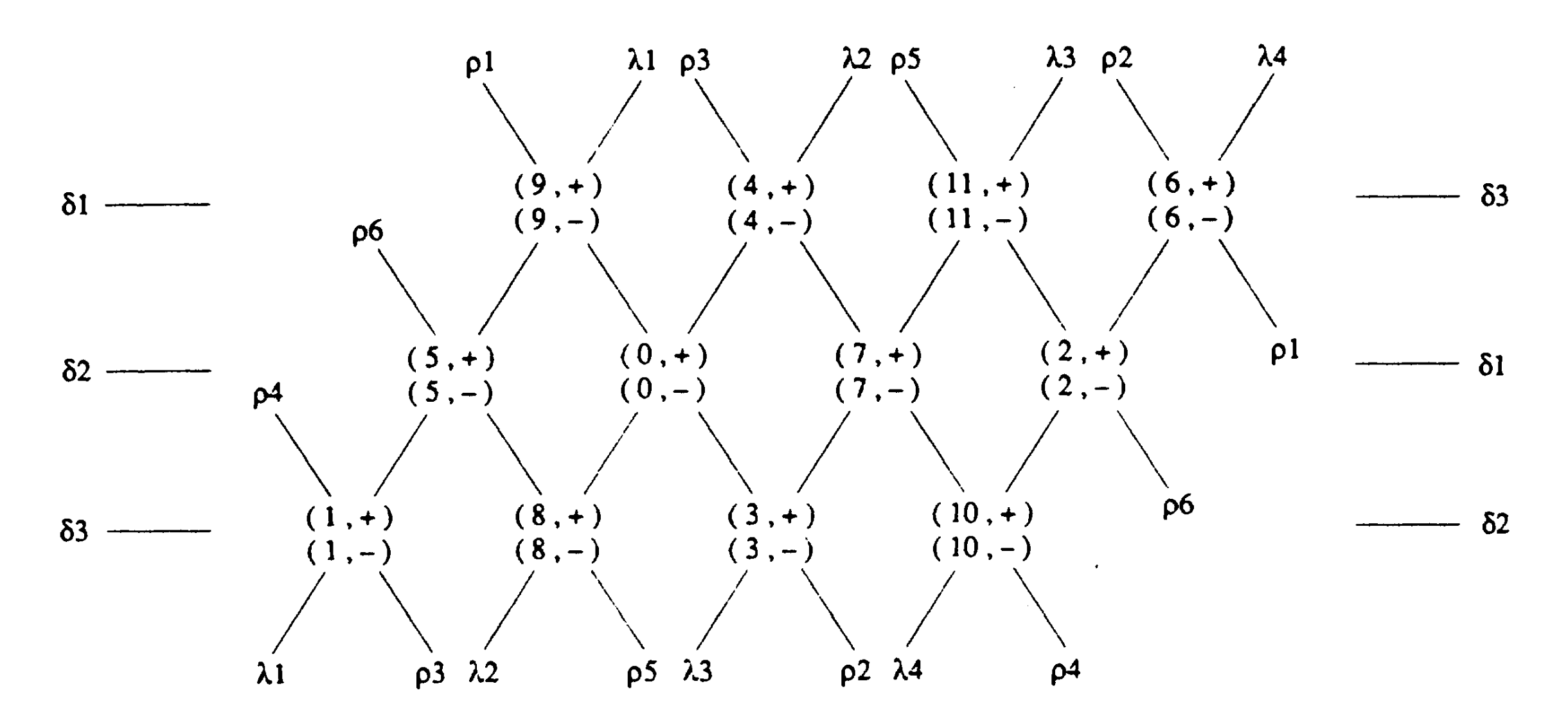
例如,音网图通常也使用这种音调级别而不是ABC音名来绘制。
Hyer, Brian. Reimag(in)ing Riemann.
写在数字旁边的±是在上一篇文章中也出现过的表示大小和弦的新里曼理论中的符号,因此(0,+)是C大和弦的意思。用数字表示音的意义很大,除了各种各样的计算操作变得容易记述之外,例如D操作的D和音名的D混淆的麻烦也能避免。
音调级集合
像音阶一样收集几个音名当然也可以用音调级来表达,那个集合叫做音调级集(英 Pitch Class Set)。Set是数学中表示“集合”的单词,也就是说“部分集合”或“基数”等,体现出欲将集合论中使用的用语全部转用到音乐理论的企图。
例如,在“Power Towers”各塔中使用的Dominant Diminish Scale的成员,如下所示用数字的集合来表示。
Douthett,Jack. Steinbach, Peter. Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.
音调级集合像这样用{}或[]括起来表示其组合。{0,1,3,4,6,7,9,10}这个数字排列的话,可以清楚地看到半全半全……的Dominant Diminish Scale的间距。另外,关于八音音阶的异名同音的拼写问题也完全不用在意。
使用音调级集在数学上发展的理论直接被称为音调级集合论(英 Musical Set Theory),这也作为与新里曼理论不同的系统理论而发展。
广义音程系统(GIS)
然后,新里曼理论的先驱大卫·勒温在1987年的著作中以广义音程系统(英 Generalized Interval Systems, GIS)为名,建议将音程的记述方法更新为更数学、更正等的东西。引用其最基本的话……
Given pitches s and t, int(s, t) is the number of scale steps one must move in an upwards-oriented sense to get from s to t. Thus int(C4, C4) = 0, int(C4,D4) = 1, int(C4,E4) = 2, and int(C4,C5) = 7. Int(C4, A3) = –2, since moving “–2 steps up” amounts to moving 2 steps down. …… This obviates a defect in the traditional measurements which tell us, for example, that a “3rd” and another “3rd” compose to form a “5th.” (3 + 3 = 5 ???)
给出音s和t,int(s, t)是从s到t的上行方向移动的音阶步数。因此int(C4, C4) = 0, int(C4,D4) = 1, int(C4,E4) = 2, int(C4,C5) = 7。Int(C4, A3) = –2,因为“向下移动2步”相当于向上移动2步。……这消除了传统测量中的一个缺陷,即“3度”和另一个“3度”组成“5度”。(3 + 3 = 5 ???)
Lewin, David. Generalized Musical Intervals and Transformations (p.16).
这里用负数代替“⚪︎度下”的说法,并且挑战解决一直困扰着我们的“零距离=1度”的问题。假设这个系统普及的话,“3度下和声”会变成“-2度和声”。在它完全取代现有系统之前,要打通这条路会相当困难,但它很有可能会像现在的“移动do”一样,成为一种持续的力量。
不管怎么样,能有这样以标准化为目标的格式是值得庆幸的,当你想用0-indexed的度数标记来写什么的时候,只说加上一句“采用勒温的GIS”就可以了。这种大家都放弃了的不便,“让我们从头再来,从我们这一代开始!”的想法这也许就是卢因的理论引起如此广泛关注的原因之一。
PLR操作的广义化
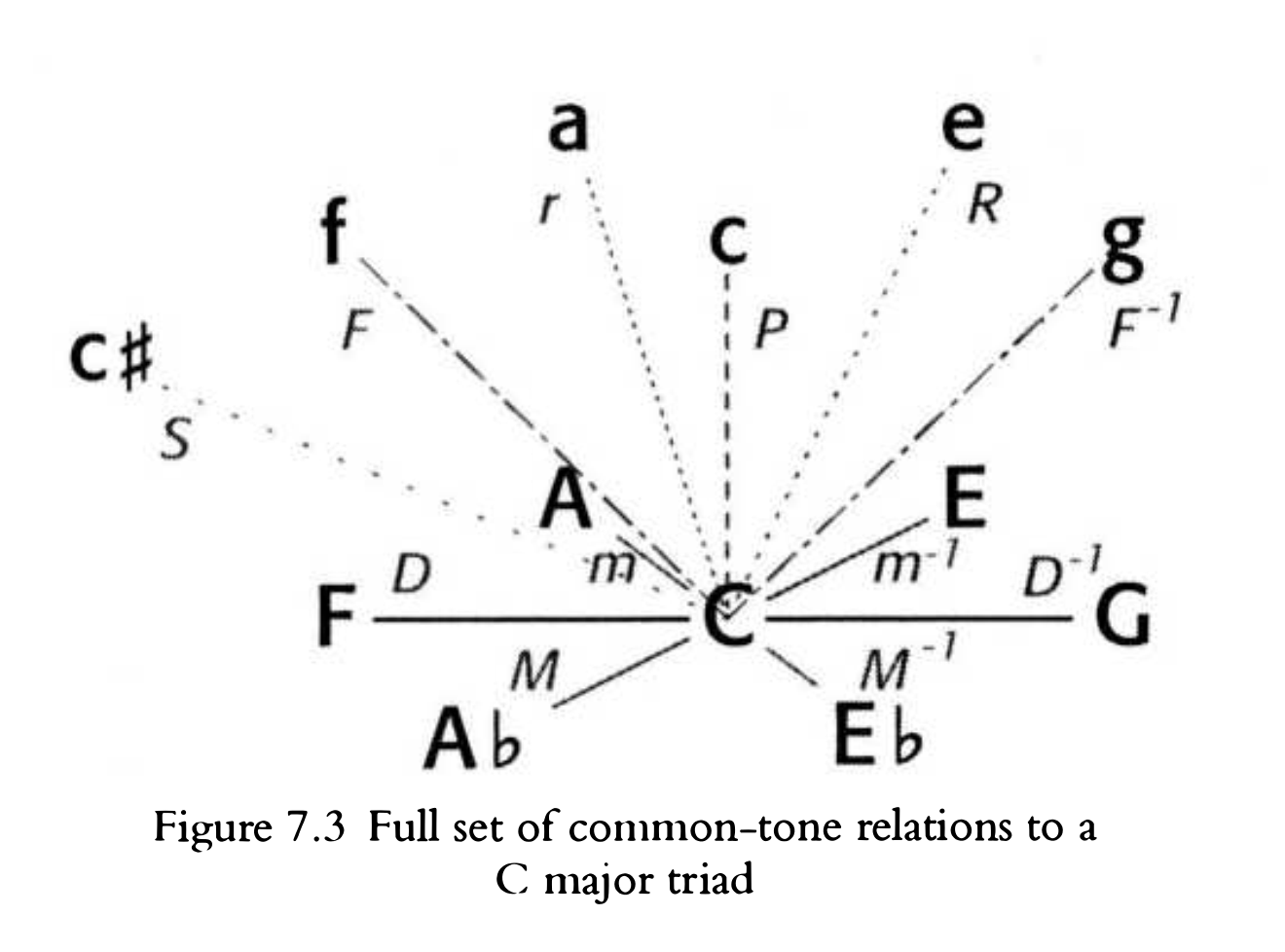
新里曼理论目前正被用于分析半音阶音乐,但作为该理论基础的PLR操作在诞生之初却是为了自然音阶,因此只有从I-vi派生的小三度下行(R)和从I-iii派生的大三度上行(L)的名称。种情况在数学上并不美观。然而,音乐学家大卫·科普(David Kopp)在其2002年出版的书中,却对这一“圣所”动了手术刀。
他提倡以根音的移动量和大小性质转换的有无为基础,对变形操作进行系统命名。
| 名称|根音变化|大小转换| |
|---|
| |M|大三度下行|无| |
| |m|小三度下行|无| |
| |R|大三度下行|有| |
| |r|小三度下行|有| |
| |D|完全五度下行|无| |
| |F|完全五度下行|有| |
所有的“下行”操作都是第一位的,“上行”都是用负1次方来表示的。M是Mediant的首字母。F来源于Fifth,前面提到的《音想像論》被翻译成英文的时候,Quint也被翻译成了Fifth。科普在这里加上P操作和S操作,把这些作为基本操作的全部。
Kopp, David. Chromatic Transformations in Nineteenth-Century Music
在这里,PLR操作中的“根据大小和弦而不同,同样的操作2次就会恢复原样”的二元论世界观被废弃了,总之优先考虑机械性。科普把这个理论命名为半音阶变形系统(英 Chromatic Transformation System),意思是与传统的二元论系统对立4
告别PLR意义重大,因为PLR是“糟粕”,拖累了自然音阶音乐观,但我个人认为,根据是否有大小转换来改变字母表并不是明智之举。不管有没有大小转换,都不认为改变字母表是个明智之举。既然习惯上用加号、减号来表示大小,那么在大小转换时使用减号会更好……不过,这也是一本20年前的书,所以现在的讨论可能更深入。
音乐的几何学
既然是用音网图和立方这样的几何学图形来表现声音,那么用几何学来讨论音乐的运动也热度高涨,其中引人注目的著作之一是德米特里·蒂莫斯科(Dmitri Tymoczko)的《A Geometory of Music》即《音乐几何学》。
这本书像勒温的GIS一样,从“把某个音高p提高χ半音的动作叫做Tχ(p)”等基本操作的函数化开始,作为在音网图画单音和和音运动的更进一步的想法,尝试2个声部的音程变化(声部连接)的图画化。

Tymoczko, Dmitri. A Geometry of Music(p.74).
这是将2音的音高组合斜着配置成坐标系,使声部连接的运动可以用线表示。故意将音程配置成斜的格子状,因为这样做的好处是,完全(度数完全相等)移动是一条真正的水平线,而完全的逆行线是一条真正的垂直线。这个空间被命名为2音的和弦空间(英 Chord Space)。声部连接由具有“长度”和“方向”两个参数的箭头表示,可以发展成声部连接的数值化和进一步的计算理论。
因为2和弦的坐标是用2维空间表示的,所以3和弦的关系可以用3维,4和弦也可以用4维来表示,在表现4维的图画hypercube(超立方体)的顶点,会表现出类似power towers的和弦图。
Tymoczko, Dmitri. A Geometry of Music(p.106).
想要从三维的角度来捕捉这个超立方体的话,自然会扭曲空间,就像在看埃舍尔的欺骗画一样,但是纯粹地关注顶点和各边的话,可以知道和cube dance一样,“同一方向的边表示相同的声音变化”的特征被充分表现出来。
另外,这本书重新审视了“调性”的定义,提出了5个要素,选取了和弦构成音的八度移动和排序等5个基本操作,根据其首字母命名为“OPTIC”,等等。这本书体现了“我要从基础重新定义”的气概。
比起这个,如果更接近数学的话,就会不断地进入“集合论”和“拓扑学”等数学专业领域,终于成为不被称为新里曼理论的另一个领域。

Alvarez, Alberto. Longoria, Pablo. A Framework for Topological Music Analysis (TMA)
包括新黎曼理论在内,这种数学化的音乐理论统称为{term:(英 {term:数学音乐理论(Mathematical Music Theory)。
4
总结
通过前面两篇文章的介绍,大家应该已经了解到,虽然统称为“新里曼理论”,但其内容和宗旨涉及的范围相当广泛。再次总结其核心话题如下。
- 把和弦的变形操作符号化。
- 关注共同音而不是根音,从声部连接的节俭性来讨论和声。
- 用图画表示单音和和声的关系,几何地论述和声。
- 将音乐理论的各种要素公式化,代数地讨论音乐。
而且论者之间互相参照文献反复讨论,即使在21世纪的今天也还在发展中。
从里曼理论到勒温理论
但是,新里曼理论的内容与里曼本来的理论相差甚远,所以经常被批评为“新里曼”这个词是将里曼的名字appropriate(使用、私有化、拥有)5
*此外,《牛津新里曼音乐理论手册》(The Oxford Handbook of Neo-Riemannian Music Theories)也将此作为一个主题进行了讨论。
例如,从根本上说,里曼的“导音转换”确实是从C引导Em的,但由此产生的Em和弦是“假装的协和和声”,与真正的Em不一样,这是其宗旨6
原本这种变形理论被称为“新里曼”的契机是先驱勒温在1982年的著作中将自己的研究称为“里曼系统”,其命名理由是“因为与里曼的研究和精神有关(associated with the spirit and work of Hugo Riemann)”,此时里曼的理论不太具体。没有继承。他在5年后的另一本书中定义了PAR和REL的操作。鉴于这些观点,熟悉里曼研究的西田紘子说了以下的话。
ここから分かるのは,ルーウィンが,リーマンの著作等を直接に参照・引用したというよりも,和声理論の代表者としてのリーマンの名を象徴的に利用したという点である。(中略) リーマンの名や概念の利用は,ルーウィンにおいて一種の権威づけとして作用し,しかもそれは成功したと言える。
由此可知,与其说勒温直接参照、引用了里曼的著作,不如说是象征性地利用了作为和声理论的代表者的里曼的名字。(中略)里曼的名字和概念的利用,在勒温作为一种权威发挥了作用,而且可以说是成功的。
西田紘子. ネオ・リーマン理論のリーマン受容にみる概念変容(p.10).
这个“有没有不正当地利用里曼的名字”的观点是相当敏感的,每个作者的叙述方式都隐晦地考虑到了这一点。
例如,上述的科普大胆地抛弃了导音转换的符号L,但此时却以“虽然舍不得丢掉”为前言,以“大和弦大写,小和弦小写是长期传统……”为挡箭牌,最终主张自己才是里曼后期理论的“忠于意向和精神”7
但不管怎样,在理论不断发展的过程中,也许是出于对一直冠以里曼之名的问题意识,他自己也给自己起了一个新的名字,叫做“半音阶变形系统”。作为更广泛的称呼,也有变形理论(英 Transformational Theory)的说法。
或者说近年来,有些人开始称为Lewinian Theory、“勒温理论”8
*又称Lewinian Toransformation、Lewinian Transformational Theory等。科普还指出,新里曼理论应被称为Lewin System
里曼好像被当做垫脚石有点可怜,但是他也站在豪普特曼和埃廷根等前人的想法上留下了自己的名字,这对音乐理论史来说是正当的流程。再过40年,也许“勒温理论”这个名字就会普及,总有一天会提倡“新勒温理论”。
谁做了什么
大致总结一下这次报道中登场的故事和人物,如下所示。
| 人物 | 主要贡献 | 主要文献 |
|---|---|---|
| Lewin | GIS的提倡。将PAR/LT/REL/DOM定义为变形操作,以及S操作也定义。 | Generalized Musical Intervals and Transformations (1987) |
| Hyer | 导入PLRD的单字化。在音网图采用Pitch Class。 | Reimag(in)ing Riemann (1995) |
| Cohn | 指出变形理论中“声部连接节俭性”的重要性。六声系统的建议。N操作的定义。除此之外还写了很多 | Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions (1996) / Audacious Euphony (2012) |
| Douthett & Steinbach | Cube Dance、Power Towers的介绍 | Parsimonious Graphs(1998) |
| Kopp | 提倡废除二元论、提出“半音阶变形系统”。 | Chromatic Transformations in Nineteenth-Century Music (2002) |
| Tymoczko | 尝试从几何学角度讨论音乐。声部连接的坐标表示。超立方体的和音网络图。 | A Geometry of Music (2011) |
当然,除了上面提到的之外,还有很多研究人员参与其中,特别是本次几乎没有提到对新里曼理论进行批评的人物等。另外,毕竟是提取了代表性的论者,所以不能否认有可能有人按时间顺序比他们更早主张上述内容。
尽管如此,感觉勒温、海尔、科恩3人是最主要的关键人物,如果想深入挖掘新里曼理论的话,首先从这3人的著作开始比较好。
到目前为止,我们介绍了爵士乐理论、古典派和声、中心轴系统和LCC,但无论哪一种都是以五度关系为理论构建的基础,五度圈总是象征着其理论美,从这个意义上说,他们完全没有多样性。
科普评价说,勒温认为属的动作不是自然法则或声音本身拥有的本有倾向,而是与音乐有关的人类故意行为(act),这是对目的论范式的强烈否定表达9
*这里所说的“目的论(teleological)”被认为是“和声进行规范预先在人类中确定,并认为它不会改变的观点”等意思。
建设中。。。