度数和泛音列
分享
1
欢迎来到古典世界
现在,我们要进入古典主义理论的主题了。在传统的古典书籍中,通常首先详细解释“度数”。更深入地理解和声原理对于学习和声是很重要的。这里也遵循这个惯例,首先详细介绍度数。从基本的复习开始,切入以前没有涉及到的科学方面。
2
度数和发声
到目前为止,我们已经在和弦篇和旋律篇中讨论了度数和发声之间的联系,但是我们会再次确认。
| ● 1度,不用多说,与根音完全协和 ● 3度,控制和弦大小的重要度数 ● 5度,与根音协和,并加强了它的声音 ● 7度,对根音产生适度的浑浊感 ● 2度,与根音发生冲突,产生强烈的不和谐 ● 4度,像五度一样,创造了一个“完美的音调”,但不像五度那样和谐 ● 6度,像三度一样,是一个影响大、小的度数 | |
|---|---|
这些故事在调性引力论的“外质”部分出现了一些。当然,还有其他“增、减”的音程,但我不会在此详述。
和弦的转位
现在再确认一下,3度的音调翻过来就是6度,4度翻过来就是5度,2度翻过来就是7度。还有一条规律是大小属性也必然会颠倒。
完全音程,翻转后仍保持完全音程。 其实不应该说“翻转”,而应该说“让一边上下八度”。例如,如果你把“三度上的和声”降低一个八度,你可以把它变成“六度下的和声”。
所以这里有一种“度数配对关系”。
色彩决定的3度、6度
基体加固的4度、5度
浑浊角色的2度、7度
这是我们第一次明确表明这一点,但是很多人应该已经有所领悟了吧?这种颠倒声音上下关系的行为,我们称之为和弦的转位(英 Inversion)。
使用3度或6度决定大小的音,使歌曲的色彩更加丰富。歌曲和声三度是最受欢迎的,因为它给我们的耳朵带来了旋律线条更加绚丽多彩的感觉。
相反,5度没有大小,而是具有加强力量的作用,这一点从“强力和弦”时就已经很明显了。
在《新しい和声》中,3度称为“柔和的声音”,完全5度称为“坚硬的声音”。这种“声音柔和、坚硬”的感觉,或者说是“声音的色彩”的感觉。要知道,这在更严格的声音叠加过程中是非常重要的。
然而,用“软”和“硬”这样的一句话来解释,总觉得有点难以释怀。当然,过去的音乐学者也不是在这种“氛围”下进行谈话的。它是在经过仔细的科学考虑之后完成的。
所以,我们有点偏离主题了,但是我们还是在这里稍微涉足一下声学(Acoustics)的话题吧。这是一个与本节无关的科学故事,如果你不感兴趣,你可以跳过它。
3
频率和音高
声音,空气的振动。声音的高度取决于它振动的速度(频率),我想我们在物理课上学过。
这是一个220hz频率的声音。声音有各种各样的声音,这是世界上最简单的声波,正弦波,我用一个叫Max的声学软件发出来的。
如果你在高中学过数学,你就会明白,这种简单波动的声音形式,可以用sin函数来表示,所以叫做正弦波。
220赫兹意味着每秒钟振动220次。220hz,用音调来说就是“la”音。一般来说这个高度的地方叫做“A3”。还有一条定律,如果你把频率加倍,就会得到恰好高于一个八度的la,我想你在物理课上也学过。
这是440hz的声音。这增加了一个数字叫做“A4”。那么,乘以3会怎样呢?我们还会升到八度吗?
这是三倍的660hz,E4。不是la,是mi的音。想想看,这很正常,因为“频率加倍会提高八度”,所以如果你想要在440hz的八度上发出声音,你必须调到880hz,这是它的两倍。
这是880hz,“A5”。1
这又是一个新的音程……这是do♯,“C♯5”的音调。我们用表格来总结这些。
| 频率 | 倍率 | 音程 |
|---|---|---|
| 220Hz | ×1 | A3 |
| 440Hz | ×2 | A4 |
| 660Hz | ×3 | E4 |
| 880Hz | ×4 | A5 |
| 1100Hz | ×5 | C♯5 |
用图表来说,就是这样。
好了,理科的实验已经结束了。想通过这个来确认什么呢,就是将某个频率加倍后最先出现的另一个音程是“完全5度”。普遍认为,频率的简单比例意味着,当我们使用和弦时,声音感觉更简单,更清晰。
这是220hz、440hz、660hz 同时发出的和音。虽然听起来可能像是两个正弦波混合在一起的声音,但是仔细听的话会发现多个音程同时响起。 用一个平易近人的话来说,就是低音,八度上的声音,以及完全5度上的声音。
不用说,这听起来非常直接,因为这是一个“强力和弦状态”。这种频率关系所产生的性质,有点诗意的表达就是“硬声响”这个词。另外,完全5度之后出现的是“大3度”,这三个就构成了大和弦,这一点也不容忽视。
频率的比例是3:4:5,这是用三和弦构成的最简单的频率比例。然后,如果你继续前进,6倍,7倍,8倍……你会看到混浊的音程,比如7度或9度。
因此,最终的“硬”这个词还是关于气氛的,我只是想说,在这个背景下,潜藏着这些科学的部分。正是依靠这些事件,音乐理论才得以考证。
4
泛音与泛音列
像这样,以某个频率为基准,然后将频率乘以整数倍的音高,这里叫做泛音(英 Overtone)。频率加倍的叫做“第二泛音”,三倍的叫做“第三泛音”等等。
另外,我们称之为倍增的原频率为基音(英 Fundamental)
| 频率 | 倍率 | 音程 | 称呼 |
|---|---|---|---|
| 220Hz | ×1 | A3 | 基音 |
| 440Hz | ×2 | A4 | 第二泛音 |
| 660Hz | ×3 | E4 | 第三泛音 |
| 880Hz | ×4 | A5 | 第四泛音 |
| 1100Hz | ×5 | C♯5 | 第五泛音 |
然后,我们把这些“泛音”按顺序排列起来,叫做泛音列(英 Overtone Series)。
以C为基音的乐谱,直到第19个泛音(频率误差大的音符显示为涂黑的音符)。
这个“泛音列”是科学思考音乐的关键,也是唯一的依据。
注意误差
但需要注意的是,对于5倍或7倍这样的泛音,它们的频率并不完全相同。例如,将440hz(la的声音)乘以7倍,得到3080hz。这一点到处都被解释为是音阶中的“sol”严格来说,在现代的一般调音中,“sol”的频率是3135hz。
事情是这样的。差不多就是这个误差吧。所以这个“泛音”理论有时候有点根本性的脆弱。
5
泛音和音色
此外,“泛音”这个词还有其他含义,因此需要注意这一点,这一点更加复杂。既然已经到了这个地步,那么也不能不解释一下,所以我再稍微说一下这个“泛音”。
这是刚才同时发出的220hz、440hz、660hz的声音,听起来绝对是单音。“音色稍微变厚的单音”。但是如果你用频率分析仪检查一下,你会发现有三堆。
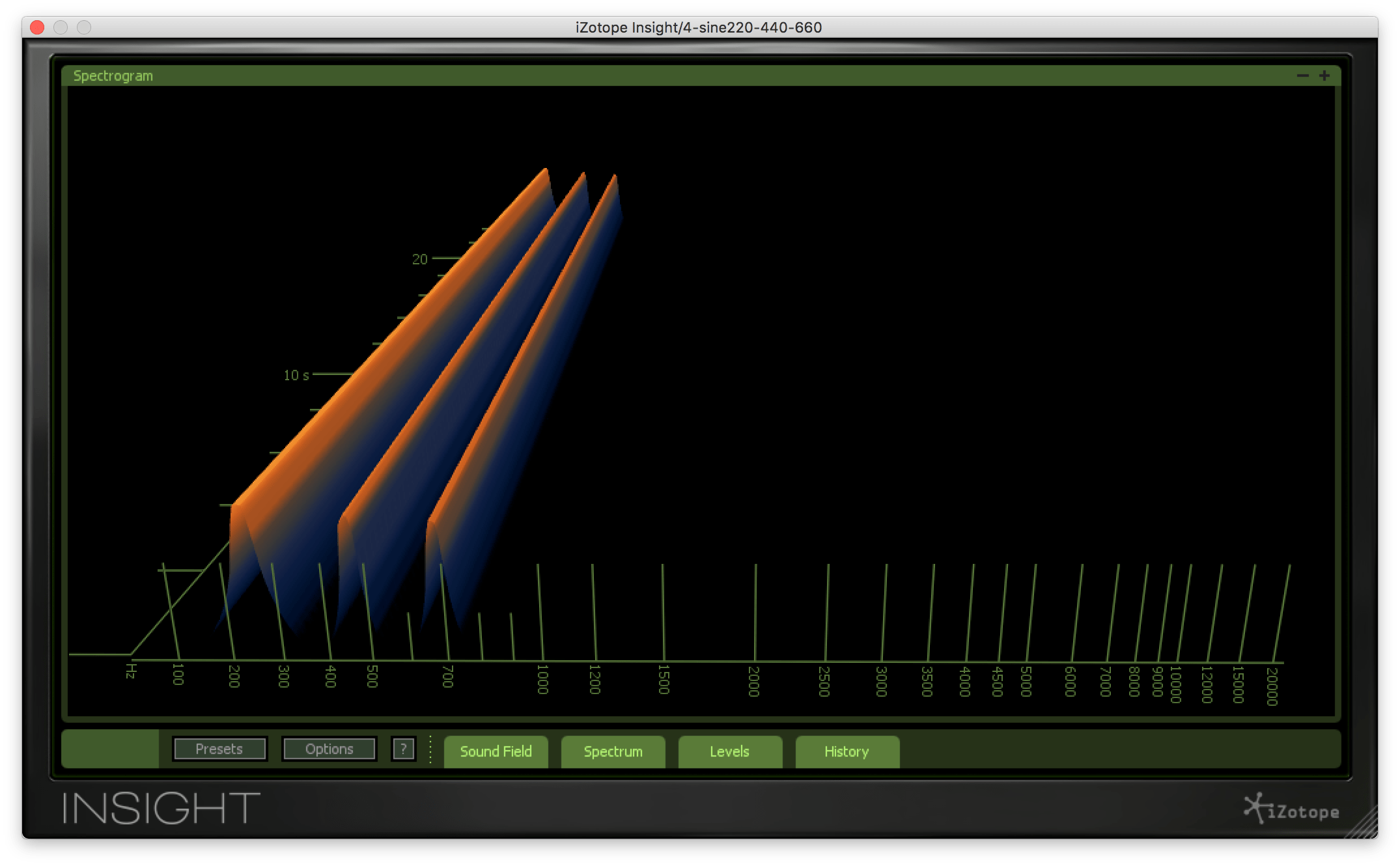
有三座山,声音却听起来像一座。这其实是理所当然的事情。
正弦波重叠与音色的关系
如果我们把基音正弦波和整数倍频的倍频波混合在一起,波之间就会混合在一起,在我们听来不是和弦,而是“音色变化的厚重声音”。这是声学的基础知识之一。
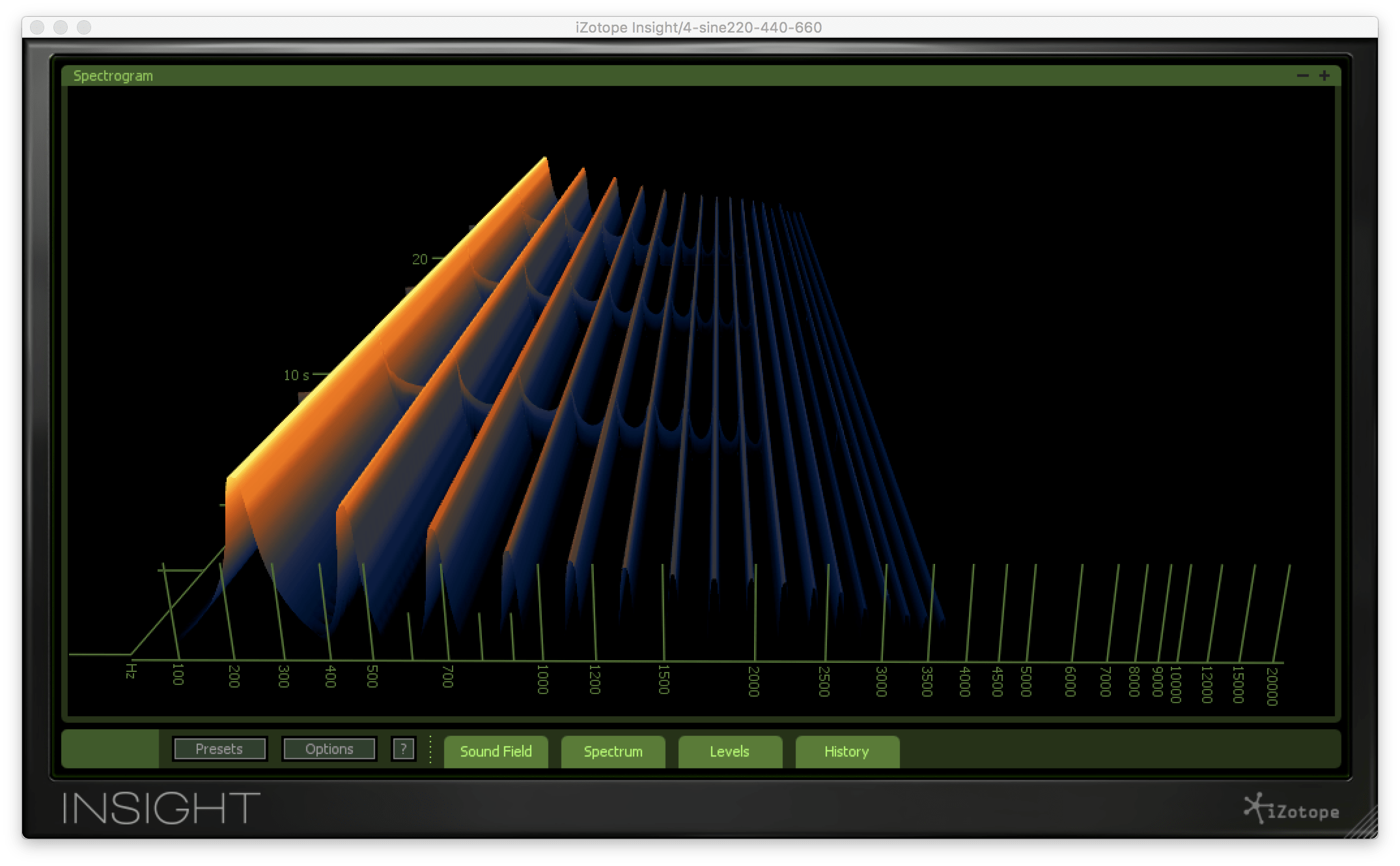
这是一个混合到第17泛音的例子。17个混在一起,听起来还是只有一个。事实上,正是因为混合了17个音高,每个音高之间才会相互碰撞,产生共鸣,产生咆哮,形成一个音色。
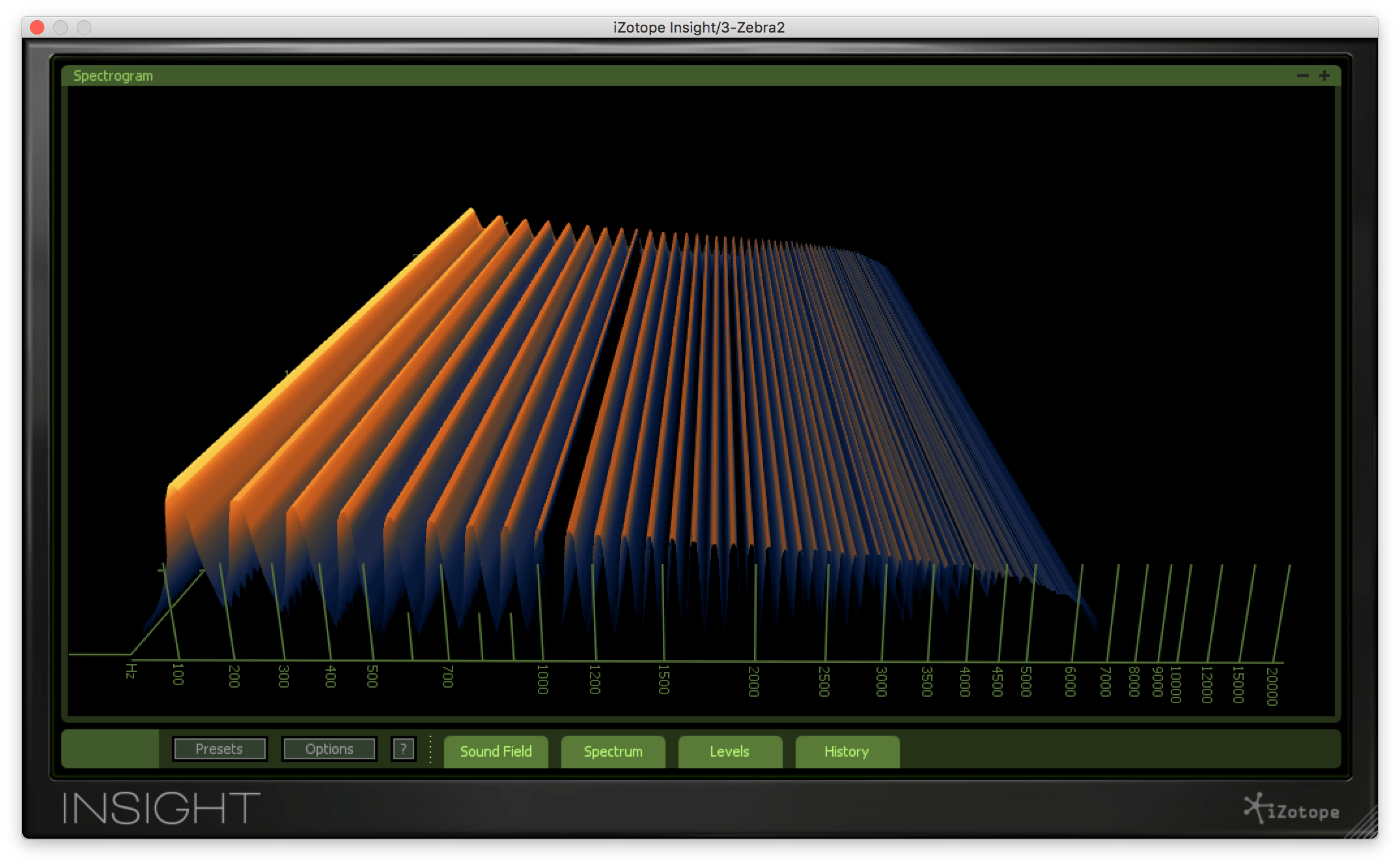
混合到第64倍的声音后,就像是用合成器经常听到的声音了。如果是220hz的64倍,那就是14080hz,这正好是与铙钹相同的高频,所以不可避免地会发出闪亮的声音。
如果你把这个放到调音器上,肯定会说”这个声音是220hz”。但是它的基音是220hz,其中有很多“隐藏的声音”,这决定了它的音色。
事实上,这不仅仅局限于电子声学合成,事实上,所有乐器都是如此。换句话说,除了调音器告诉我们的主音高(基音)之外,还有许多泛音同时发出,这些泛音的分配决定了音色。
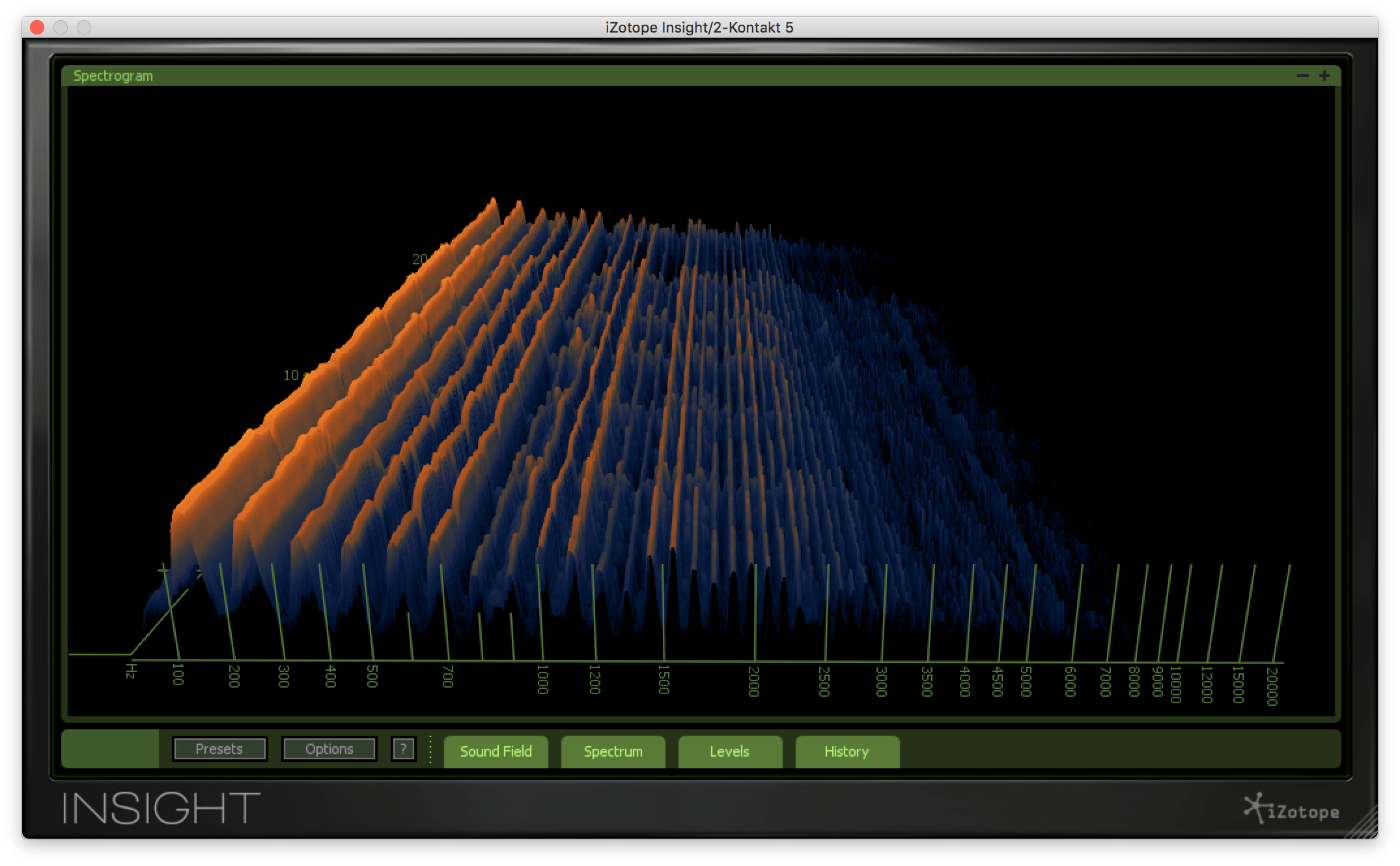
然而,自然界的这种声音比合成器创造的音色要复杂得多。这是大提琴的声音,你可以看到,非常细微的泛音混合在一起,而且声音的发出方式也有波动。即使在计算机技术最发达的今天,也很难模拟这种复杂的泛音结构,这就是为什么市场上很少有软件能够通过计算机运算再现乐器的声音。
顺便说一句,当非整数倍频率混合时,声音会越来越接近噪声。
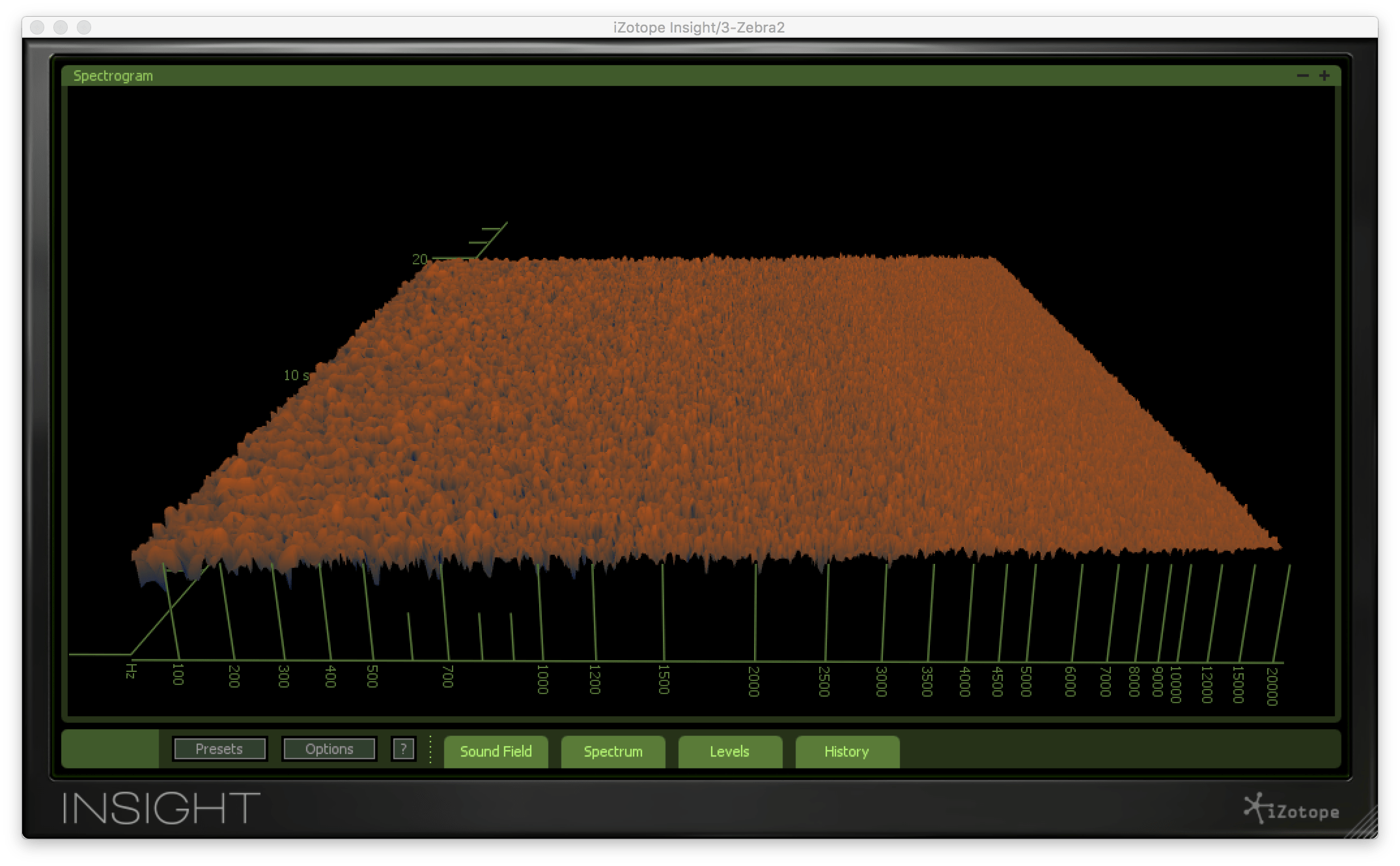
这里是白噪声频率分析。像云一样均匀分布,所以不存在音高感。没有音高的声音就是噪音。打击乐的声音也会有这样的频率而且,在刚才的大提琴中,弦的摩擦声也是噪音,这与音色的丰富性息息相关。
从这里衍生出来的,有时用“泛音”这个词来表示“音色”之类的意思,这也是一种混淆。
虽然泛音的故事说来话长,在了解真正的音乐理论的过程中,一定会遇到“这里的泛音”,所以是时候介绍一下了,所以在这里登场了。现在忘了也没关系。只要以后在某个地方出现科学话题时,记得这里提到过足够了。
不管怎么说,几百年前的人们研究了这些麻烦的科学部分,我们从中受益匪浅。然后,让我们更加意识到不同度数的颜色和质感的差异,然后继续前进。
总结
-
两个音符的和声因程度不同而有很大的差异,八度的单音和完全五度的和声是非常直接的一致。
-
从科学的角度来看,5度和8度声音的简单性多少有些说服力。
-
把一个声音作为“基音”,把它的频率乘以整数的声音称为“泛音”。
-
“泛音”是对各种音乐理论进行科学考证的基础。
建设中。。。